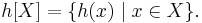Amalgamation property

In the mathematical field of model theory, the amalgamation property is a property of collections of structures that guarantees, under certain conditions, that two structures in the collection can be regarded as substructures of a larger one.

An amalgam can be formally defined as a 5-tuple (A,f,B,g,C) such that A,B,C are structures having the same signature, and f: A → B, g: A → C are injective morphisms that are referred to as embeddings.

A class K of structures has the amalgamation property if for every amalgam with A,B,C ∈ K and A ≠ Ø, there exist both a structure D ∈ K and embeddings f': B → D, g': C → D such that

A simple example would be the class of sets with embeddings just being injective functions has the amalgamation property (with amalgam simply the union of the two sets). Another example would be the class of free groups with embeddings being injective homomorphisms has the amalgamation property, where the amalgam is just the quotient group , where * is the free product.

A notion in model theory that is similar to the amalgamation property (although different) is the joint embedding property.

The diagram of the amalgamation property appears in many areas of mathematical logic. Examples include in modal logic as an incestual accessibility relation, and in lambda calculus as a manner of reduction having the Church-Rosser property.

Strong amalgamation property

A class K of structures has the strong amalgamation property (SAP) if for every amalgam with A,B,C ∈ K there exist both a structure D ∈ K and embeddings f': B → D, g': C → D such that

and

where for any set X and function h on X,

See also

• Age (model theory)
• Span (category theory)
• Pushout (category theory)

References

• Hodges, Wilfrid (1997). A shorter model theory. Cambridge University Press. ISBN 0-521-58713-1. 
• Entries on amalgamation property and strong amalgamation property in online database of classes of algebraic structures (Department of Mathematics and Computer Science, Chapman University).